速寫 Day50

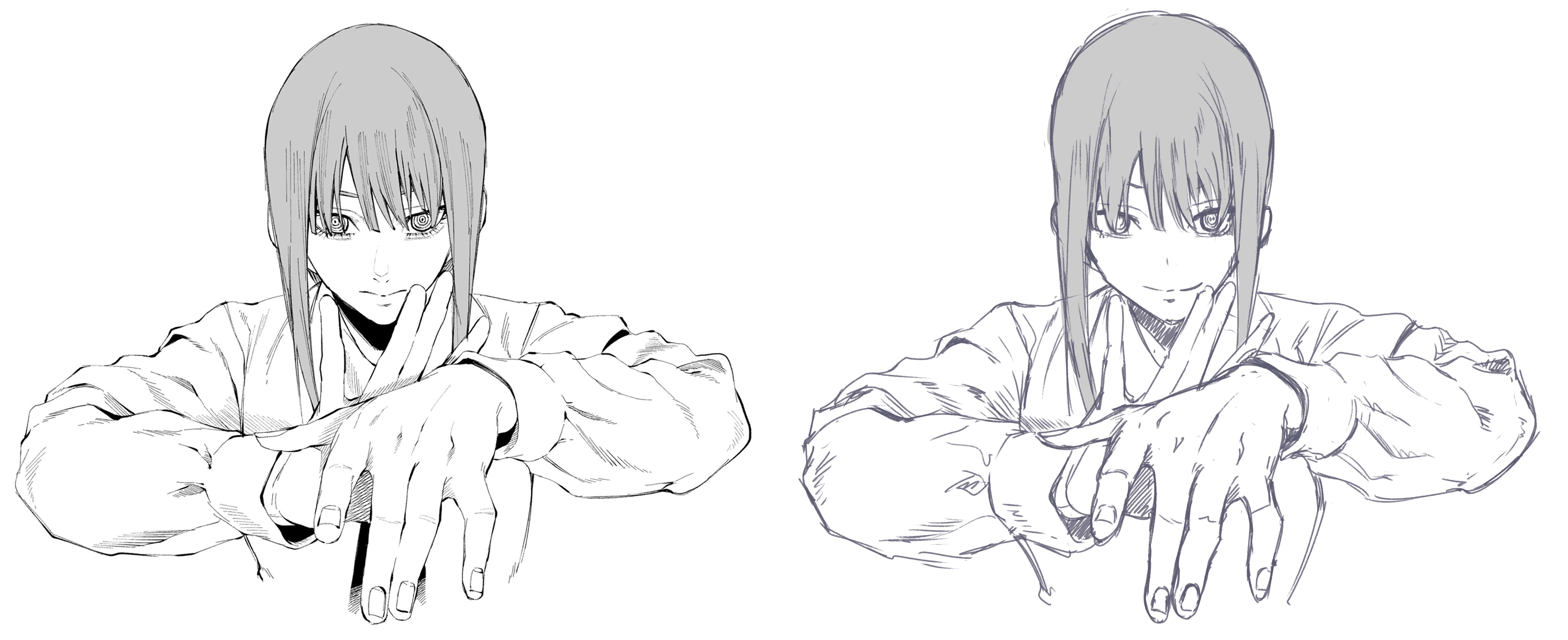
依舊是沒速寫day，
放瑪奇瑪壓壓驚。
個人真的是私心喜歡這張臨摹。
~~是因為裝潢還沒完全好。~~
~~真的不是因為我懶==~~

Inference stage: use training data to learn a model for \(p(C_k|x)\)
Decision stage: use these posterior probabilities to make optimal class assignments.
Generative models: approaches that explicitly or implicitly model the distribution of inputs as well as outputs.
-> can detect outlier/novelty because it can model the distribution.
Discriminative models: approaches that model the posterior probabilities directly.
Maximizing joint probability \(p(x,C_k)\) is equivalent to maximizing posterior probability \(p(C_k|x)\) because \(p(x)\) is common to all terms.
Minkowski loss function: a simple generalization of the squared loss: \(E(L_q)=\int\int |y(x)-t|^qp(x,t)dxdt\)

Kullback-Leibler divergence \(KL(p||q)=\int p(x)ln(\dfrac{q(x)}{p(x)})dx \geq 0\) if and only if \(p(x)=q(x)\).
We can try to approximate the distribution using some parametric distribution \(q(x|\theta)\), governed by a set of adjustable parameters \(\theta\), by minimizing the KL divergence between \(p(x)\space and\space q(x|\theta)\)
Conditional entropy of y given x: \(H(x,y)=H(y|x)+H(x)\)

–

Mutual information: the reduction in the uncertainty about x by virtue of being told the value of y.
\(I(x,y)=-\int\int p(x,y)ln(\dfrac{p(x)p(y)}{p(x,y)})dxdy\), and \(I(x,y)\geq0\) if and only if x and y are independent.
\(I(x,y)=H(x)-H(x|y)=H(y)-H(y|x)\)

我會繼續努力的。